В этой лабораторной работе многократно будет использоваться стек, поэтому для начала предлагается освежить в памяти, как эта структура обычно выглядит на языке python.

Упражнение №1

Напишите программу, которая последовательно кладет в стек произвольный массив чисел, а затем распечатывает их , последовательно доставая, пока стек не пуст (например, набор (1,...,10)).

Правильные скобочные структуры

Известно, что скобочные выражения могут быть корректными и некорректными. Корректные - это такие, которые можно вычислить по правилам, если расставить между ними числа и знаки бинарных операций. Иными словами, интуитивно, такие. где зоны действия скобок разных типов не пересекаются(если есть скобки разных типов).

Упражнение №2

Написать программу, определяющую правильность введенного скобочного выражения, в котором используются скобки 3 видов: (), {}, /.

Арифметические выражения. Инфиксная, постфиксная и префиксная нотации

Рассмотрим арифметическое выражение: \begin{equation*} (2-3)*(12-10)+4/2 \end{equation*}

Его значение легко вычисляется и оказывается даже целым - это 0(не забываем правила приоритета операций!). Это привычная для нас форма записи арифметических выражений, в которой если операция бинарная (т.е. требует 2 аргументов, например, сложение, деление), то один аргумент пишется перед знаком операции, а другой - после неё. Такая форма записи называется инфиксной.

Нотация (способ записи), в которой операнды пишутся перед знаком операции - называется постфиксной или обратной польской.

Нотация. в которой операнды пишутся после знака операции - прямой польской или префиксной.

Например, уже рассмотренное выражение в обратной польской записи будет выглядеть как

\begin{equation*} 2 3 - 12 10 - * 4 2 / + \end{equation*}

После пары 2 и 3 стоит знак вычитания. После пары 12 и 10 - тоже. Далее стоит знак перемножения, потому что результаты этих двух операций надо умножить. Далее стоят 4 и 2 и после них знак деления. А после - знак сложения, показывающий, что результат предыдущего нужно сложить с результатом деления 4 на 2.

а в прямой польской как

\begin{equation*} + * - 2 3 - 12 10 / 4 2 \end{equation*}

Аналогичным образом, только теперь знак операции стоит перед операндами (или их описаниями в виде выражений в той же форме записи).

Упражнение №3

Перевести выражение

\begin{equation*} (3+4*(2-1))/5 \end{equation*}

в прямую и обратную польские записи.

В общем и целом, любое выражение можно представить в виде структуры, называемой деревом(синтаксическим деревом в данном случае, поскольку оно отражает структуру выражения). Например, для разобранного выражения синтаксическое дерево будет выглядеть так:

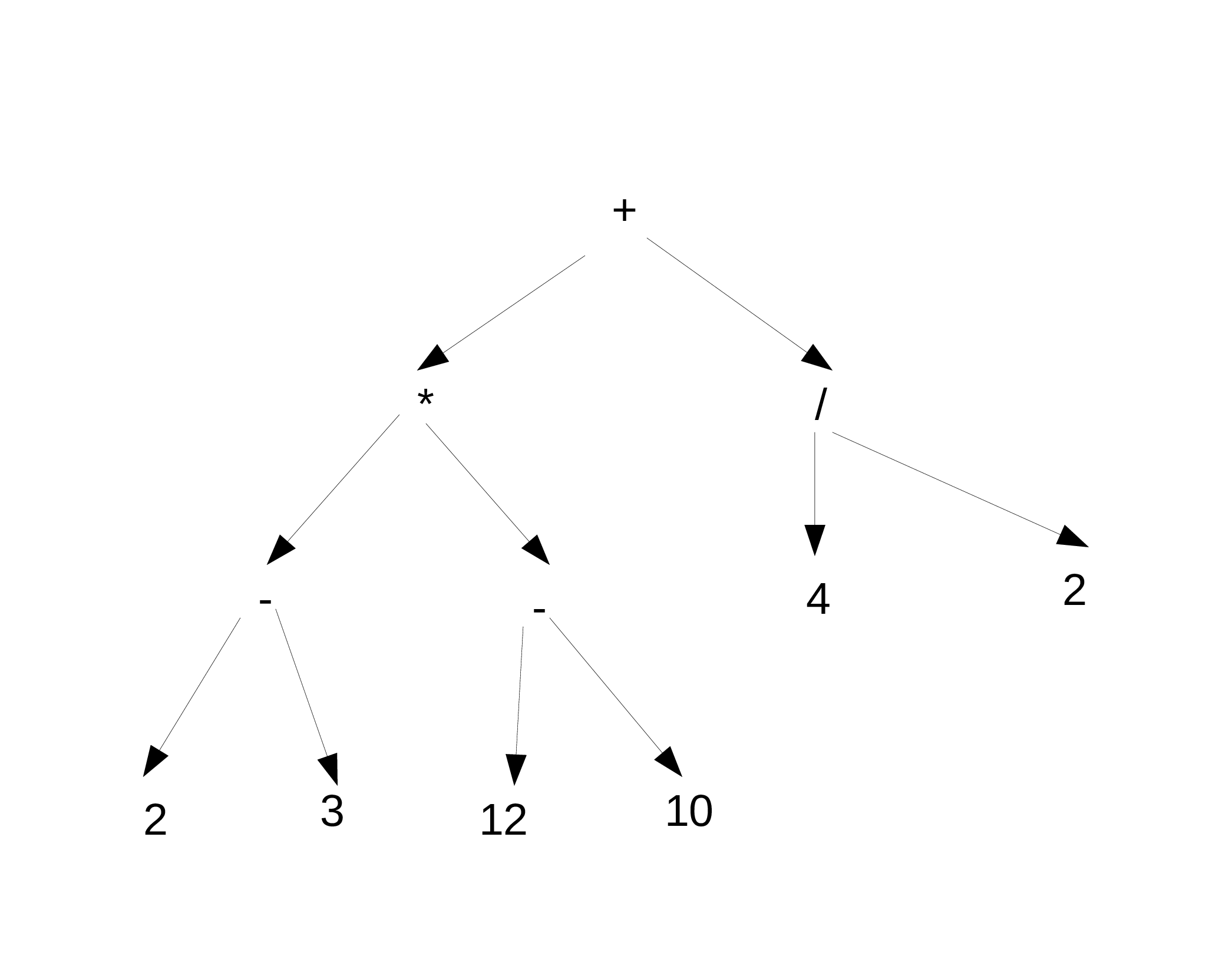
Его конечные вершины, листья (из которых стрелки никуда не идут) - это операнды, а промежуточные (из которых идут стрелки)- операции. Прямая польская запись (префиксная) получается, если читать это дерево сверху вниз. Обратная (постфиксная) - если читать снизу вверх.

Стековый калькулятор

Стековый калькулятор - это устройство (реальное или виртуальное), которрое вычисляет значения арифметических выражений , записанный в постфиксной форме. Стековым он называется по понятным причинам: если нам встречается число - мы должны поместить его в стек; если знак опренрации - мы должны достать из стека столько чиссел, скольок необходимо для выполнения данной операции. Именно так и работает т.н. математический сопроцессор (например, в INtel8086+AMD64)- часть ЦП, отвечающая за операции над числами с плавающей запятой.

Упражнение №4

Реализовать стековый калькулятор на python. Написать программу, которая читает выражение в обратной польской нотации и считает его значение или пишет, что выражение составлено не корректно (если оно некорректно).

Сортировочная станция Дейкстры

Как нетрудно видеть: выражения в обратной польской записи удобны для чтения компьютером , но неудобны для чтения и составления людьми. Поэтому хотелось бы доверить труд составления постфиксной формы выражений по их привычной инфиксной форме компьютеру. Это можно сделать с помощью так называемого алгоритма сортировочной станции (Shunting Yard algorithm , придуман Э. Дейкстрой в 1961 году, см https://en.wikipedia.org/wiki/Shunting-yard_algorithm для трансляторов языка Algol60 https://ir.cwi.nl/pub/9251).

В следующем примере, взятом как раз из википедии, разбирается преобразование выражения

\begin{equation*} a+b*c-d \end{equation*}

Есть сортировочная станция с 3 путями: 2 подъездных и 1 тупик. С правоого подъездного пути едут выражения: в каждом "вагоне" или операнд или знак операции. Операнды свободно проезжают в левый путь (образуя очередь), а операторы заезжают в тупик.

By Salix alba - Own work, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=10960619

Если приоритет входящего оператора ниже приоритета того, что навершине стека (на входе в тупик), то из стека достаётся оператор с большим приоритетом (на шаге g это умножение). То же самое происходит, если приооритет приходящего оператора равен приоритету такового на вершине стека, но тот, что на вершине - ассоциативен. В данном случае после отъезда умножения остаётся сложение, приоритет которого равен приоритету вычитания, но сложение в отличие от вычитания ассоциативно:

\begin{equation*} (a+b)+с=a+(b+c) (a-b)-c!=a-(b-c)=a-b+c \end{equation*}

Упражнение №5

Реализовать на python алгоритм сортировочной станции для преобразования произвольных арифметических выражений с 4 действиями (+,-,*,/) из инфиксной записи в обратную польскую.

Упражнение №6(*)

Добавить в предыдущую реализацию поддержку выражений со скобками.

Практика: Арифметические выражения и калькуляторы

Скобочные выражения, Обратная польская запись, стековый калькулятор

Стеки