Рекурсия: фракталы
Рекурсия
Как мы видели раньше функции могут вызывать другие функции — это вполне обыденная ситуация. При этом функция может вызывать саму себя. Такой тип вызова называется рекурсивным. Самый простой пример рекурсивного вызова функции — вычисление факториала числа:
>>> def fac(n):
... if n == 0:
... return 1
... else:
... return n * fac(n - 1)
...
>>> fac(5)
120
Конечно, эту программу можно переписать и без рекурсивных вызовов:
>>> def fac(n):
... f = 1
... x = 2
... while x <= n:
... f *= x
... x += 1
...
... return f
...
>>> fac(5)
120
Отличие этих двух программ кроется в подходе к их построению. Первая написана в декларативном стиле, то есть для
вычисления факториала используются его свойства, а именно n! = n*(n-1)! и 0!=1. Второй же подход использует
императивный стиль: мы явно описываем, что представляет из себя факториал: n! = 1*2*…*n. В большинстве случаев
один и тот же алгорит может быть легко записан, как в рекурсивной форме, так и в нерекурсивной, но существует ряд задач,
для которых построение нерекурсивного алгоритма представляется весьма трудозатратным.
Количество вложенных рекурсивных вызовов называется глубиной рекурсии. В силу ограниченности вычислительных ресурсов
рекурсия в компьютерных программах не бывает бесконечной — программист должен явно следить за тем, чтобы глубина
рекурсивных вызовов не превышала заранее известного числа. Если программист об этом не позаботился (или же сделал это
некорректно), операционная система (или интерпретатор) аварийно завершит программу по исчерпанию доступых ресурсов.
Чтобы убедиться в этом, попробуйте вычислить (-5)! при помощи рассмотренного ранее примера рекурсивного алгоритма
вычисления факториала.
Модуль sys обеспечивает доступ к некоторым переменным и функциям, взаимодействующим с интерпретатором python
и операционной системой.
Упражнение №1: длина рекурсии
С помощью функции fac(n) определите текущую установленную глубину рекурсии и сравните ваш результат с возвращаемым значением функции sys.getrecursionlimit(). Учтите, что sys.getrecursionlimit() возвращает максимальную глубину стека вызовов, а не максимальную глубину рекурсии для какой-либо функции.
Упражнение №2: числа Фибоначчи
Напишите программу, вычисляющую n-ное число Фибоначчи. Используйте рекурсивные вызовы функций. Пример
| Ввод | Вывод |
|---|---|
| 7 | 13 |
Черепашка
В следующих заданиях снова будет использоваться модуль turtle. Напомним полезные функции из этого модуля:
| Команда | Значение |
|---|---|
| forward(X) | Пройти вперёд X пикселей |
| backward(X) | Пройти назад X пикселей |
| left(X) | Повернуться налево на X градусов |
| right(X) | Повернуться направо на X градусов |
| penup() | Не оставлять след при движении |
| pendown() | Оставлять след при движении |
| shape(X) | Изменить значок черепахи (“arrow”, “turtle”, “circle”, “square”, “triangle”, “classic”) |
| stamp() | Нарисовать копию черепахи в текущем месте |
| color() | Установить цвет |
| begin_fill() | Необходимо вызвать перед рисованием фигуры, которую надо закрасить |
| end_fill() | Вызвать после окончания рисования фигуры |
| width() | Установить толщину линии |
| goto(x, y) | Переместить черепашку в точку (x, y) |
Фракталы
Хорошим примером для иллюстрации рекурсивных алгоритмов являются задачи рисования фракталов. Фрактальные кривые, обладающие бесконечным самоподобием, не являются спрямляемыми: хоть их и можно изобразить на плоскости конечной площади, эти кривые имют бесконечную длину. Соответственно, программно их невозможно нарисовать полностью: всегда будет возможность нарисовать кривую детальнее. Поэтому, фрактальные кривые рисуют в некотором приближении, заранее фиксируя максимально допустимую глубину рекурсии.
Пример программы, использующей рекурсивные вызовы функции, чтобы нарисовать ветку:
import turtle
def draw(l, n):
if n == 0:
turtle.left(180)
return
x = l / (n + 1)
for i in range(n):
turtle.forward(x)
turtle.left(45)
draw(0.5 * x * (n - i - 1), n - i - 1)
turtle.left(90)
draw(0.5 * x * (n - i - 1), n - i - 1)
turtle.right(135)
turtle.forward(x)
turtle.left(180)
turtle.forward(l)
draw(400, 5)
Результат выполнения программы при разной глубине рекурсии:



Упражнение №3: кривая Коха
Нарисуйте кривую Коха. Процесс её построения выглядит следующим образом: берём единичный отрезок, разделяем на три равные части и заменяем средний интервал равносторонним треугольником без этого сегмента. В результате образуется ломаная, состоящая из четырёх звеньев длины 1/3. На следующем шаге повторяем операцию для каждого из четырёх получившихся звеньев и т. д… Предельная кривая и есть кривая Коха.
Пример работы алгоритма при разной глубине рекурсии:




Для ускорения рисования используйте:
turtle.speed('fastest')
Упражнение №4: снежинка Коха
Три копии кривой Коха, построенные (остриями наружу) на сторонах правильного треугольника, образуют замкнутую кривую бесконечной длины, называемую снежинкой Коха. Нарисуйте ee.
Пример работы алгоритма при разной глубине рекурсии:




Упражнение №5 кривая Минковского
Нарисуйте кривую Минковского. Кривая Минковского нулевого порядка - горизонтальный отрезок. Затем на каждом шаге каждый из отрезков заменяется на ломанную, состоящую из 8 звеньев.
Пример работы алгоритма при разной глубине рекурсии:



Упражнение №6: кривая Леви
Нарисуйте кривую Леви. Она получается, если взять половину квадрата вида /\, а затем каждую сторону заменить таким же фрагментом и так далее.
Пример работы алгоритма при разной глубине рекурсии:




Упражнение №7: кривая дракона
Нарисуйте кривую дракона. Кривая дракона нулевого порядка - горизонтальный отрезок. Разделим отрезок пополам и построим на нем прямой угол, получив кривую дракона первого порядка:

На сторонах прямого угла снова построим прямые углы. При этом вершина первого угла находится справа от начальной точки A, а направления, в которых строятся вершины остальных углов, чередуются.
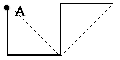
Примеры:


Упражнение №8: Канторово множество
Нарисуйте Канторово множество. Канторово множество нулевого порядка - горизонтальный отрезок. Удалив среднюю треть получим множество первого порядка. Повторяя данную процедуру получим остальные множества.


